Aktuell unterstütze ich für meinen Arbeitgeber, die Cassini Consulting einen IT-Dienstleister bei der Realisierung einer kundenspezifischen Software-Plattform, gebildet aus Mitteln der JEE (Spring, JMS, JPA). Im Zuge dieses Projektes werden auch Analyse-Werkzeugen eingesetzt, welche Aspekte des objekt-orientierten Designs erfassen und (graphisch) aufbereiten. Getreu dem Motto „a fool with a tool is still a fool” ist für mich vor allem der theoretische Hintergrund von Bedeutung.
Metriken
Viele der eingesetzen Werkzeuge (wie JDepend, CAP, SonarJ) verwenden Metriken, die bereits 1994 von Robert Martin als OO Design Quality Metrics1 definiert wurden. Die maßgeblichen Kennzahlen dabei sind:
- die Abstraktheit (abstractness, A) einer Kategorie
- die Instabilität (instability, I) einer Kategorie
- die Distanz (distance, D) einer Kategorie zur Ideallinie, der sog. main sequence
Der Begriff „Kategorie” beschreibt in diesem Kontext eine logische Gruppierung innerhalb der Architektur, hierbei könnte es sich z.B. um eine Java Library, ein Java Package oder ein Maven Modul handeln.
Abstraktheit
Die Abstraktheit wird nun aus dem Verhältnis von „abstrakten” (Na) zur Summe aller Klassen gebildet (abstrakte und „konkrete”, Nc). Im Java-Kontext schließt die Qualifizierung als „abstrakt” dabei auch Interfaces mit ein. Es gilt:
A = Na : (Na + Nc)
Der Wertbereich ist [0,1], kann also als Prozentzahl wiedergegeben werden. 0% bedeutet, das die Kategorie ausschließlich aus konkreten Klassen besteht, 100% bedeutet, daß die Kategorie ausschließlich aus abstrakten Klassen oder Interfaces besteht.
Instabilität
Zur Bestimmung der Instabilität verwendet R. Martin die Abhängigkeiten einer Kategorie von anderen Kategorien. Dabei unterscheidet er zwischen eingehenden Abhängigkeiten (afferent couplings, Ca) und ausgehenden Abhängigkeiten (efferent couplings, Ce).
Afferent couplings sind also Abhängigkeiten, welche andere Kategorien in die betrachtete Kategorien haben, efferent couplings sind Abhängigkeiten, welche die betrachtete Kategorie in andere Kategorien hat.
Wieder wird das Verhältnis gebildet, es gilt:
I = Ce : (Ce + Ca)
Auch hier kann der Wertebereich [0,1] in Prozent ausgedrückt werden. Je mehr ausgehende Abhängigkeiten eine Kategorie hat, desto höher ist der Grad an Instabilität. I ist also 0 für Kategorien, die keinerlei ausgehende Abhängigkeiten haben und 1 für Kategorien, die ausschließlich ausgehende Abhängigkeiten haben.
Main Sequence
Die für eine Kategorie ermittelte Abstraktheit A und Instabilität I lassen sich hervorragend als Achsen eines Graphen verwenden. Jede Kategorie kann dann als Koordinate in das System eingetragen werden. Doch welche Aussage lässt sich aus ihrer Plazierung machen?
- A=1, I=0
- eine Kategorie, die zu 100% abstrakt ist und keinerlei ausgehende Abhängigkeiten hat, ist eine API. Interfaces und abstrakte Klassen definieren dabei die notwendigen Operationen, welche durch eine konkrete Implementierung zu realisieren sind
- A=0, I=1
- eine Kategorie, die zu 0% abstrakt ist und ausschließlich abgehende Abhängigkeiten hat, ist eine Implementierung. Am Ende der Vererbungskette realisiert sie z.B. eine API
- A=1, I=1
- eine Kategorie, die zu einem hochgradig abstrakt ist und andererseits ausschließlich abgehende Abhängigkeiten hat, stellt keinen erstrebenswerten Zustand dar. Als API ist sie zu instabil, als Implementierung müssten konkrete Klassen vorhanden sein
- A=0, I=0
- Kategorien, welche stabil und konkret sind, haben ihre Berechtigung als geschlossenes, kleines System. Ein klassisches Beispiel dafür ist das typische HelloWorld.java, lässt man die Abhängigkeiten zu den JRE/JEE Bibliotheken außen vor. In größeren Architekturen wird dieser Punkt vermutlich nie erreicht werden.
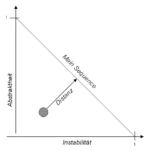
In der Theorie von R. Martin bildet die Strecke zwischen den Extremen von A und I nun die sog. Main Sequence (A + I = 1). Sie beschreibt das Verhältnis zwischen Abstraktheit und Instabilität, welches als ausgewogen (balanced) gilt.
Distanz
Die oben beschriebenen Kennzahlen dienen bisher nur der Einordnung einer Kategorie in den Graphen. Zur Bestimmung der „Güte” einer Kategorie empfiehlt R. Martin nun die Berechnung der Distanz (distance) einer Kategorie von der main sequence. Es gilt:
D = |(A + I – 1) : 2|
oder einfacher (um einen Wert zwischen 0 und 1 zu erhalten):
D = |A + I – 1|
Ziel des objekt-orientierten Design sollte es nun sein, die Distanz nahe an 0 zu bringen, etwa indem man ausgehende Abhängigkeiten eliminiert und damit die Stabilität erhöht, oder Kategorien in APIs mit hoher Abstraktheit und Implementierungs-Bereiche unterteilt.
Fazit
Die oben aufgeführten Metriken können eine Hilfe beim objekt-orientieren Design bzw. der objekt-orientierten Analyse sein. Man sollte sich ihnen aber nicht blind unterwerfen, denn wie immer gilt: Das Ideal im Blick, das Projektziel unter den Fingern.
1 Robert Martin: OO Design Quality Metrics – An Analysis of Dependencies, 1994
Schreibe einen Kommentar